学习笔记-4

OpenFOAM programming tutorial

Valid asymmetric matrix solvers are :
GAMG
PBiCG
PBiCGStab
smoothSolver
Valid symmetric matrix solvers are :
GAMG
PBiCGStab
PCG
smoothSolver

OpenFOAM中的基本线性方程组求解器

求解器，预处理，光顺器 目的：

  1. 了解lduMatrix的结构；
  2. 比较DIC/FDIC预处理器；
  3. 建立多重网格求解器；
$ src
$ ls
Allwmake                genericPatchFields  rigidBodyMeshMotion
atmosphericModels       lagrangian          sampling
combustionModels        mesh                semiPermeableBaffle
conversion              meshTools           sixDoFRigidBodyMotion
dummyThirdParty         ODE                 sixDoFRigidBodyState
dynamicFvMesh           OpenFOAM            surfMesh
dynamicMesh             OSspecific          thermophysicalModels
engine                  parallel            topoChangerFvMesh
fileFormats             Pstream             transportModels
finiteVolume            randomProcesses     triSurface
functionObjects         regionCoupled       TurbulenceModels
fvAgglomerationMethods  regionModels        waves
fvMotionSolver          renumber
fvOptions               rigidBodyDynamics

cd OpenFOAM/
$ ls
algorithms  dimensionedTypes  global   interpolations  matrices  primitives
containers  dimensionSet      graph    lnInclude       memory
db          fields            include  Make            meshes
$ cd matrices/
$ ls
DiagonalMatrix  LUscalarMatrix  RectangularMatrix  SquareMatrix
lduMatrix       Matrix          scalarMatrices     SymmetricSquareMatrix
LduMatrix       MatrixBlock     simpleMatrix       tolerances
LLTMatrix       QRMatrix        solution
$ cd lduMatrix/
$ ls
lduAddressing  lduMatrix  preconditioners  smoothers  solvers

进入solvers文件夹，有如下求解器：diagonalSolver GAMG PBiCG PBiCGStab PCG smoothSolver

  • diagonalSolver - diagonal solver for both symmetric and asymmetric problems
  • GAMG - Geometric agglomerated algebraic multigrid solver
  • PBiCG - Preconditioned bi-conjugate gradient solver for asymmetric lduMatrices using a run-time selectable preconditioner
  • PbiCGStab -New preconditioned bi-conjugate gradient stabilized solver for asymmetric lduMatrices
  • PCG-Preconditioned conjugate gradient solver for symmetric lduMatrices using a runtime selectable preconditiioner
  • smoothSolver - Iterative solver using smoother for symmetric and asymmetric matrices which uses a run-time selected smoother
  • 矩阵合并；
  • 网格同矩阵间的通讯；
  • lduMatrix类；
  • OpenFOAM中的求解器；
  • Krylov sub-space methods
  • BICG方法；
  • BiCGSTAB案例

矩阵来源于控制方程的离散，可归为fvScalarMatrix; fvVectorMatrix; fvTensorMatrix，例如

fvVectorMatrix UEqn
(
fvm::ddt(U)
+ fvm::div(phi, U)
- fvm::laplacian(nu, U)
);

系数矩阵A来源于fvm运算符：

  • 对角元素来源于空间离散；
  • 非对角元素为临近单元贡献；
  • 方程右边的元素来源于源项（fvc运算符）或者旧时间步数据；

OpenFOAM中的方程求解总是遵循如下模式：

  • 初始化；
  • 整合矩阵；
  • 求解；
  • 修正；

接下来对icoFoam中的方法进行距离举例说明：

/*---------------------------------------------------------------------------*\
Application
    icoFoam

Description
    Transient solver for incompressible, laminar flow of Newtonian fluids.

\*---------------------------------------------------------------------------*/

#include "fvCFD.H"
#include "pisoControl.H"

// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

int main(int argc, char *argv[])
{
    #include "setRootCaseLists.H"
    #include "createTime.H"
    #include "createMesh.H"

    pisoControl piso(mesh);

    #include "createFields.H"
    #include "initContinuityErrs.H"

    // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

    Info<< "\nStarting time loop\n" << endl;

    while (runTime.loop())
    {
        Info<< "Time = " << runTime.timeName() << nl << endl;

        #include "CourantNo.H"

        // Momentum predictor

        fvVectorMatrix UEqn//创建fvVectorMatrix类实例UEqn
        (
            fvm::ddt(U)
          + fvm::div(phi, U)
          - fvm::laplacian(nu, U)
        );//初始化;

        if (piso.momentumPredictor())
        {
            solve(UEqn == -fvc::grad(p));//求解
        }

        // --- PISO loop
        while (piso.correct())//修正
        {
            volScalarField rAU(1.0/UEqn.A());
            volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));
            surfaceScalarField phiHbyA
            (
                "phiHbyA",
                fvc::flux(HbyA)
              + fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)
            );

            adjustPhi(phiHbyA, U, p);

            // Update the pressure BCs to ensure flux consistency
            constrainPressure(p, U, phiHbyA, rAU);

            // Non-orthogonal pressure corrector loop
            while (piso.correctNonOrthogonal())
            {
                // Pressure corrector

                fvScalarMatrix pEqn
                (
                    fvm::laplacian(rAU, p) == fvc::div(phiHbyA)
                );

                pEqn.setReference(pRefCell, pRefValue);

                pEqn.solve(mesh.solver(p.select(piso.finalInnerIter())));

                if (piso.finalNonOrthogonalIter())
                {
                    phi = phiHbyA - pEqn.flux();
                }
            }

            #include "continuityErrs.H"

            U = HbyA - rAU*fvc::grad(p);
            U.correctBoundaryConditions();
        }

        runTime.write();

        Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s"
            << "  ClockTime = " << runTime.elapsedClockTime() << " s"
            << nl << endl;
    }

    Info<< "End\n" << endl;

    return 0;
}


// ************************************************************************* //

Mesh ⇔ Au = b

  • 显然矩阵A和网格有强关联；
  • 网格数量等于A的秩；
  • 元素来源于数值离散权重；
  • 总的而言，A为稀疏矩阵；
  • 对角元数个数等于网格个数；
  • 非零上半三角矩阵和下半三角矩阵元数个数等于网格内表面数；
  • 上半三角矩阵元素属于owner faces;
  • 下半三角矩阵元素属于neighbour faces;
  • 如果一个面被Owner单元和neighbour单元共享，则对应一个矩阵非对角非零元素；

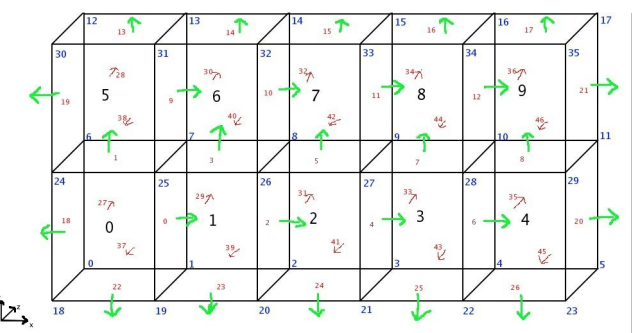
有限体积离散将存储为lduMatrix类，其中fvMatrix为lduMatrix子类；我们通常处理的矩阵都为稀疏矩阵；非零元素将存储在三个arrays中：lower();diag()以及upper(); 例如前面的矩阵中，有如下arrays：

lower () = (a1,0 , a5,0 , a2,1 , a6,1 , a3,2 , a7,2 , a4,3 , a8,3 , a9,4 , a6,5 , a 7,6 , a8,7 , a9,8)
diag () = (a0,0 , a1,1 , a2,2 , a3,3 , a4,4 , a5,5 , a6,6 , a7,7 , a8,8 , a9,8)
upper () = (a0,1 , a0,5 , a1,2 , a1,6 , a2,3 , a2,7 , a3,4 , a3,8 , a4,9 , a5,6 , a6,7 , a7,8 , a8,9)

矩阵的求解需要改善系数矩阵A的性质，可以以A的条件数为判断依据，cond(A)越接近1，则迭代求解过程越容易收敛；为了使矩阵方程容易求解，目的可转化为寻找矩阵M，使得M-1Ax=M-1b; 为了加速矩阵求解速度，可进行预处理：

  • diagonalPreconditioner for symmetric & nonsymmetric matrices (not very effective)
  • DICPreconditioner Diagonal Incomplete Cholesky preconditioner for symmetric matrices
  • DILUPreconditioner Diagonal Incomplete LU preconditioner for nonsymmetric matrices
  • FDICPreconditioner Fast Diagonal Incomplete Cholesky preconditioner
  • GAMGPreconditioner Geometric Agglomerated algebraic MultiGrid preconditioner
  • noPreconditioner 器：
  • BICCG Diagonal incomplete LU preconditioned BiCG solver*
  • diagonalSolver Solver for symmetric and nonsymmetric matrices
  • GAMG Geometric Agglomerated algebraic Multi-Grid solver
  • ICC Incomplete Cholesky Conjugate Gradient solver
  • PBiCG Bi-Conjugate Gradient solver with preconditioner
  • PCG Conjugate Gradient solver with preconditioner
  • smoothSolver *Iterative solver with run-time selectable smoother
  • GMRES: The Generalized Minimal RESidual algorithm is the first method to try if A is not SPD.
  • BiCG: The BiConjugate Gradient algorithm applies to general linear systems, but the convergence can be quite erratic.
  • BiCGstab The stabilized version of the BiConjugate Gradient algorithm. *Most of these solvers are Krylov-subspace solvers.

本文总阅读量次 ⤧  Next post openfoam学习笔记-5 ⤧  Previous post openfoam学习笔记-3